A good many book have been written on this topic and, being involved professionally with both mathematic and music, I had many good polite party conversations that invariably start with: "But of course, Mathematics and Music are so similar", or “How interesting, so many mathematicians are also musicians!”. After that, being the somewhat direct Italian that I am, I generally proceed to try to explain why the relationships is actually very tenuous, and in so doing manage to ruin a perfectly fine party atmosphere.

So ... Why is the relationship tenous? Leaving to the side the fact that there are probably way more physicians than mathematicians doing music, I always found somewhat of a misconception at the root of the math&music debate. People, from innocent party goers all the way to the 60’s composer writing pieces with titles such as “Quantum Field” or “Theorem in Four Parts”, seem to either be a bit misinformed about what mathematics is really about, or at best to be confusing music with … acoustics.

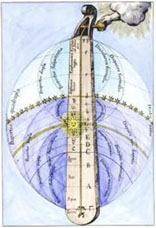
A lot of acoustics can of course be represented using mathematical relationships. The ancient Greek, in the western hemisphere, started to do so thousands of years ago.  But even earlier, Paleolithic men built flutes in the pentatonic scale, and that implies knowledge of at least some interval relationships. Acoustic lingered at the level of mathematical description codified by the Greek for millenia. It even got a bit esotheric. People like Robert Fludd, in the early 17th century, described the celestial monochord, a construction that links the Ptolemaic, geocentric, universe to musical intervals. (The celestial monochord is shown in the figure above.) Then the scientific revolution and calculus exploded and swapped away the charming planetary alchemies. From the 19th century to this day mathematical models have been used to represent all kinds of sounds and sound properties with increasing leavels of accuracy.

But, to make a blunt statement: unlike sound no musical composition can be described using mathematics. Paleolithic men knew how to build an instrument by drilling holes, at specific points, on a hollow branch of wood, but once that was achieved no “mathematics” was involved in generating the lost melodies that filled their days.

To elaborate a bit, I think that there are at least two main reasons why mathematics has nothing to do with composition. The first is that the laws of acoustics have little to do with the craft of composition. To draw a parallel: acoustics are to music as bricks and mortar are to architecture. One can describe mathematically bricks and mortar, and engineer many different variations for specific purposes, but no architect can build using those properties alone. One can even add all the laws of gravity, and detail very precise mathematical descriptions of all the structural constraints that a building must satisfy to be structurally viable. But still one would only be able to build the most trivial structures, if any, based only on those laws and descriptions. Greeks built temples, but there is no mathematical reason why those magnificent buildings were built in ways that still touch us emotionally. Composition, from a mathematical point of view, has even fewer constraints than architecture: there a no laws of gravity, there are no hard structural constrains.

But there is a second, and deeper, reason. Mathematics, as so beautifully put by Haruki Murakami, is the kingdom of infinite consistency: it is a land ruled by numbers, logic and theorems. In the land of mathematics solutions exist, and they are incontrovertible. The arts, and life, do not work like that. No matter how clear the relationship of things might become in a story, or a painting, or a composition, there is never a clear-cut solution to those relationships. Art, at most, seems to take a problem and translate it, change the perspective, look at it from one side, than another.  Ancient and modern temples are built as symbols, hints at solutions to the fundametal question of what is our place in the world. The math involved in their construction is completely incidental.

So … Why Math & Music? It is because of the bricks. I am interested in building some musical bricks that are a bit different from what we currently have (or that I am aware of), and some math might be able to help in that regard.

: