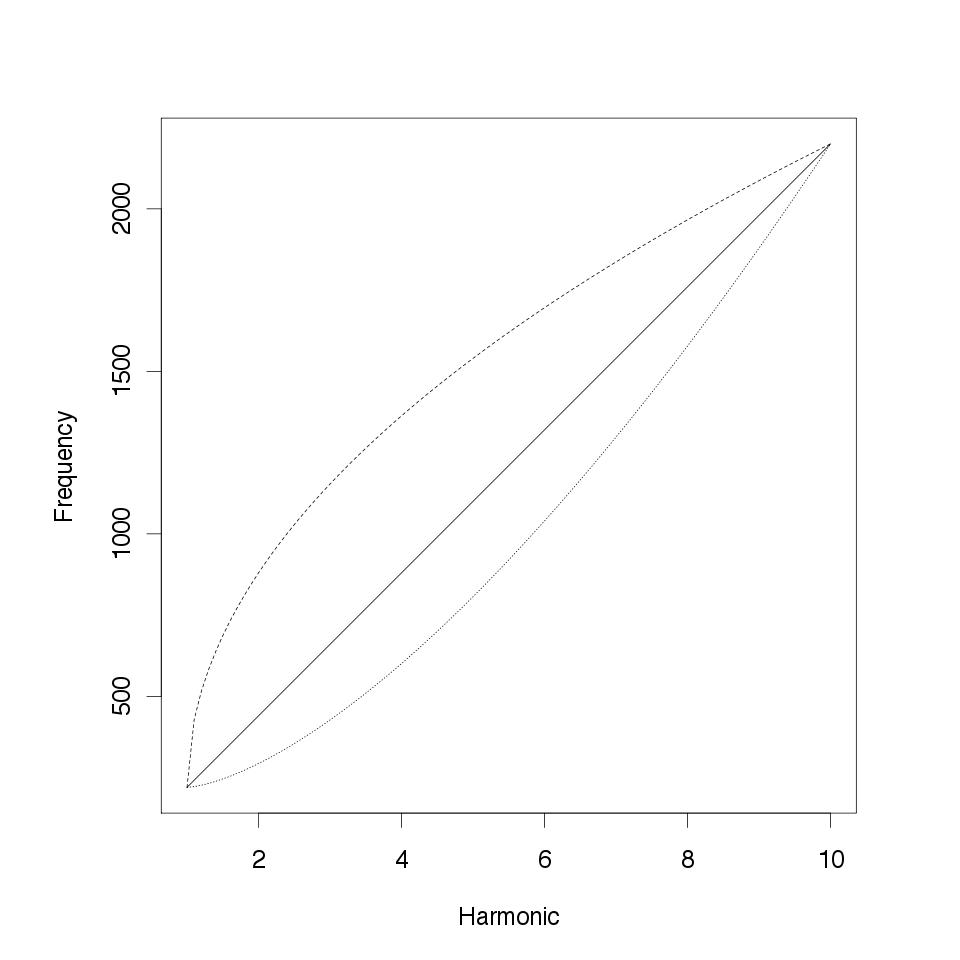
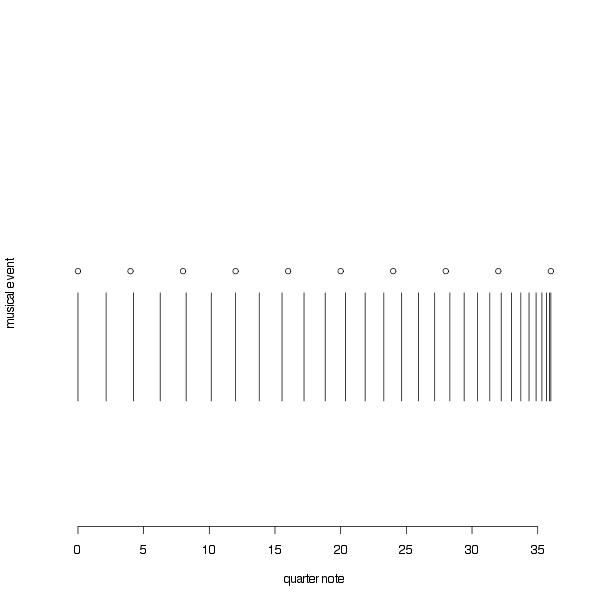
|
The harmonic series is generated by a linear relationship of the form $f_k =f_b k$, where $f_b$ is the fundamental frequency and $k = 1, 2, ...$. From a compositional view point harmonic series have been used relatively recently, for example by the spectral school in the 1960-70s. From a compostional point of view the aims of the in-harmonic series that are described below are somewhat similar to the aims of the spectralists. Similarly to the spectralist I (i) generate harmonic material, "chords", from the series I devise, and in addition I (ii) explicitely derive "scales" from the "chords", in both cases this is done to generate materials that can be used for composing. The chords that are generated usingthe in-harmonic series can be used functionally (although at the time of this writing I have not completely worked out how to do so), or structurally, i.e..simply as "locations" that are reached during the itinerary of a composition. The "scales" serve the original function of traditional scales and arpeggios: to connect musical materials that are located in different locations in frequency/pitch domain of a composition. The first step in the creation of the inharmonic series is using to change the linear relationship depicted above to a power low of the form: $f_k = f_b \left( 1 +( \frac{k-1}{n-1})^{\gamma} (n-1) \right)$, $k = 1, 2, ...$ when $\gamma$=1 the relationship obtains the harmonic series, otherwise it produces a series that grows faster or slower than lineraly depending on the value of $\gamma$ (as depicted in the figure below). The chords are obtained using $n=11$ harmonics, a number that generates a rich natural harmonic series that includes the augmented triad. They can be classified according to their dissonance value that is reported at the top of the figure and computed as described here (the values of dissonance for each chord are read left to right, top to bottom). Under each chord are also reported the scales that can be obtained from the corresponding series. Different series (and scales) are obtained for different values of $n$. either the ordered collection of the unique pitches making up a chord or sections of the chord played melodically, I used inharmonicity in Midday, where I use the following two chords: The chords are obtained using n=11 (left) and n=12 (right) harmonics. The parameter $\gamma$ determines the rate of growth of the inharmonic series. The value of dissonance reported in the figure is for reference only. Midday is a piece for wind quintet, characterized by un ascent from the lowest to the highest pitches of the two chords. Because the ensemble prvides only five possible voices the chords as depicted are never heard in their entirety in the piece. The scales that are obtained from the corresponding series are reported under each chord. In Ultramarinus for orchestra I use again inharmonic series, but I also include their transpositions. In the same piece I occasionally use accellerandos obtained using a simple power law. The accelerandos take forms as in the figure below, where a vertical bar indicates a musical event (e.g. a new pitch) and the open circles mark the measure bar. The power law is simply: Time of Event $= n x^\gamma$ where $n$, in this case, is the number of quater notes, $x$ an equispaced sequence with length equal to the total number of events, $x \in [0,1]$, $\gamma$ is a parameter that determines the rate of acceleration. When $\gamma = 1$ we obtain (metric) events spaced at quarter notes.
Inharmonic series and related scales
The figure reported below shows the chords that are obtained by altering the harmonic series using a relationship between the fundamental and the harmonics that grows slower than linearly. The figure shows the chords for different value of a parameter ($\gamma $) that determines the rate of growth from the fundamental. When $\gamma$=1 (upper left chord) we obtain the harmonic series,for $\gamma > 1$ intermediate frequencies between the 1st and 11th harmonic, are shifted to lower values. (All pitches shown in the figure are rounded to the nearest equal temperament pitch.)
 |
||
|
