
 |
12 or 88+? Ernst Toch (The Shaping Forces in Music. Dover, New York 1977 (first ed. 1947), pg. 64) comments on an important distinction between harmonic and melodic pitch: "While it is correct to say that the twelve tones of our chromatic scale exhaustively present the material of all their harmonic potential, it is not correct to say that they exhaustively present the material of all melodic potentialities as well. We may acknowledge the multifarious of harmonies drawn from the twelve tones of an octave; but we succumb to grave fallacy if we apply the same consideration to melody". He continues: "though it is completely irrelevant harmonically whether we deal with any tone or with its higher or lower octave, it makes all the difference melodically". The 88+ pitches available in western tuning, are indeed distinct entities (notes). The fact that notes at an octave distance are easily identifiable, and that they are characterized by a certain frequency ratio (1:2), does not make them less distinctly different then notes at the distance of a fifth, a 9th or a 74th. We hear a difference between A2 and A4, as well as we hear the difference between A2 and D3. The reasons why A2 and A4 are different is not only associated with their fundamental frequency, but also with their resonating frequencies (harmonics). To show this, instead of producing table comparing frequncies we are going to look at the harmonics directly using a spectrogram. The following figure shows a spectrogram for the sequence of notes A0, A1, ... , A7. The figure gives a nice illustration of the differences between A0, ... , A7. If one takes into consideration the harmonics these pitches appear to be very different not only melodically (fundamental pitch) but also harmonically. There is a big difference in the density of harmonics present in any given frequency interval, for any given fundamental. For example in the interval 818-1356 we see 3 harmonics for A3, 2 for A4, 5 for A6. This is expected, remember that for a given fundamental (eg. A3 at 220Hz) the harmonics are the (infinite) series composed simply by its multiples. For A3, the harmonic series is 220, 440, 660, 880, 1100, 1320, 1540, ... . For A4 it is 440, 880, 1320, 1760 ... . Note the the series do not match. A4 is less rich harmonically then A3, and A2 is much less so and so on: higher notes are litterally missing harmonic components in respect to lower ones. Is this of consequence for the harmonic treatment of musical material? I am inclined to think so, that is: I am not only agreeing with Toch (melodically octave equivalence make little sense), but my intuition tells me to go an extra step, harmonically whether we deal with a note or with its higher or lower octave might not be irrelevant. Unless a composer artificially limits his horizon, melodies have access to 88+ notes. Does a composer have more then 12 notes at its disposal, harmonically? We hear the differences when the same pitch is at lower and higher octave. The difference is even more striking when we consider chords. and these differences correspond to very different harmonics aggregates, as seen above for single notes. Could octave equivalent chords imply different harmonic functions, or be treated differently? ... 88+? The following figure shows a spectrogram for two A major and minor chords. Figure 2: Spectrogram (log scale) for A major (upper panel) and minor (lower panel) chords with fundamental A2 and A4, respectively. The chords are generated using Finale and the Garritan Steinway samples. Each chord is of the same duration (13.5") and dynamic intensity.

The importance of register is immediately recognizable if one transposes a pitch in any melody just one octave lower or higher: the melody is drammatically altered but the 'harmonies' (generally speaking: any other supporting pitch) are unchanged, and still make sense for any given harmonic style of writing. 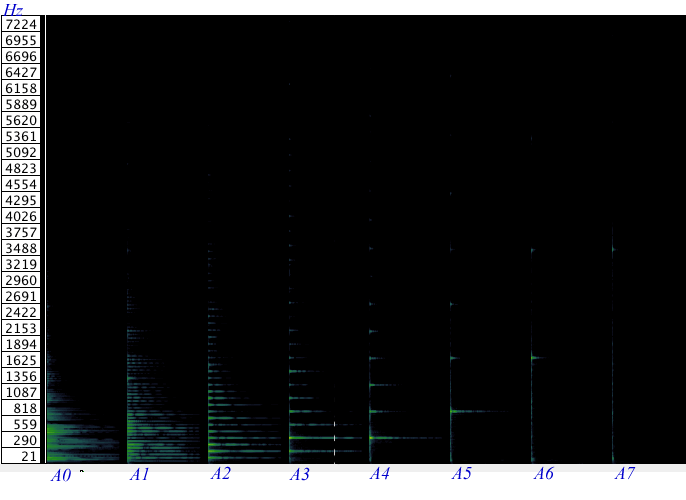
Figure 1: Spectrogram of the note sequence A0,A1,...,A7. The notes are generated using Finale and the Garritan Steinway samples. Each note is of the same duration (13.5") and dynamic intensity.

 |
||
|